When calculating the output impedance we still assumed an infinite
input impedance.
In this section we will calculate the finite input impedance assuming
a zero output impedance.
We consider a model that assumes an internal resistor ![]() connecting the inverting and non-inverting input terminals of the
op-amp as shown in figure 6.31
connecting the inverting and non-inverting input terminals of the
op-amp as shown in figure 6.31
Consider an inverting amplifier and remove the input resistor so that the input impedance can be calculated directly at the amplifier's input terminals.
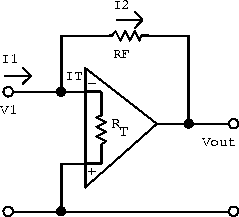
Figure 6.31: Model for calculating the input impedance of
the inverting amplifier.
The input impedance is defined by
![]()
and the current at the summing junction is
![]()
The current through the feedback resistor is
![]()
and the output voltage is related to ![]() by the open-loop gain
by the open-loop gain
![]()
The resulting input impedance is thus
![]()
For large A
![]()
The closed-loop input impedance is thus small and almost independent of
the large ![]() of the operational amplifier.
of the operational amplifier.
Now consider the non-inverting amplifier shown in figure 6.32.
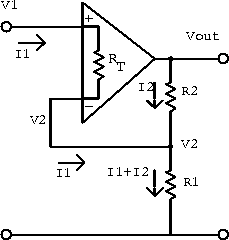
Figure 6.32: Model for calculating the input impedance of
the non-inverting amplifier.
The student should calculate the input impedance by recognizing that
![]() is much less than
is much less than ![]() , since
, since ![]() is much greater
than
is much greater
than ![]() or
or ![]() .
Your result should be
.
Your result should be
![]()
where ![]() is the closed-loop gain of the amplifier.
Notice that in contrast to the low input impedance for the inverting
amplifier, the non-inverting amplifier exhibits a closed-loop input
impedance that is much larger than the open-loop value
is the closed-loop gain of the amplifier.
Notice that in contrast to the low input impedance for the inverting
amplifier, the non-inverting amplifier exhibits a closed-loop input
impedance that is much larger than the open-loop value ![]() .
.