The binary 0 and 1 states are naturally related to the true and false logic variables. We will find the following Boolean algebra useful. Consider two logic variables A and B and the result of some Boolean logic operation Q. We can define
![]()
Q is true if and only if A is true AND B is true.
![]()
Q is true if A is true OR B is true.
![]()
Q is true if A is false.
A useful way of displaying the results of a Boolean operation is with
a truth table.
We will make extensive use of truth tables later.
If no ``-'' is available on your text processor or circuit
drawing program an ``N'' can be used, ie. ![]() .
.
We list a few trivial Boolean rules in table 7.2.
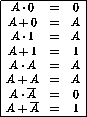
Table 7.2: Properties of Boolean Operations.
The Boolean operations obey the usual commutative, distributive and associative rules of normal algebra (table 7.3).
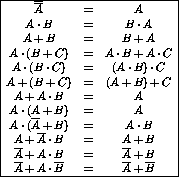
Table 7.3: Boolean commutative, distributive and
associative rules.
We will also make extensive use of De Morgan's theorems (table 7.4).
![]()
Table 7.4: De Morgan's theorems.