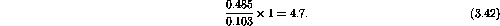As before, consider expanding the transfer function as the ratio of two polynomials
![]()
If ![]() are the roots of
are the roots of ![]() and
and ![]() are
the roots of
are
the roots of ![]() we can write
we can write
![]()
where A is a real constant, ![]() are zeros of
are zeros of ![]() and
and
![]() are poles (infinities) of
are poles (infinities) of ![]() .
Knowledge of
.
Knowledge of ![]() and
and ![]() determines
determines ![]() everywhere.
everywhere.
Lets now look at our two filter circuits. For a low-pass filter
![]()
and the filter has one pole at -1/(RC). For a high-pass filter
![]()
and it has one pole at -1/(RC) and one zero at 0. We refer to these two types of filters as single-pole filters.
There is a general rule that there must be at least as many reactive elements as poles. Based on the location of the poles we are able to deduce the general response properties of the filter. We will not do this here.
Example: If a transfer function has poles atand
and a zero at (0,0), as shown in figure 3.5,
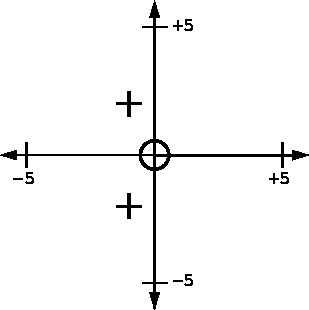
Figure 3.5: Poles and zeros in the complex plane.
- sketch
on the interval
.
The transfer function is given by

Plugging in values for
gives the table 3.1.
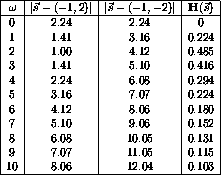
Table 3.1: Numerical values of the transfer function.
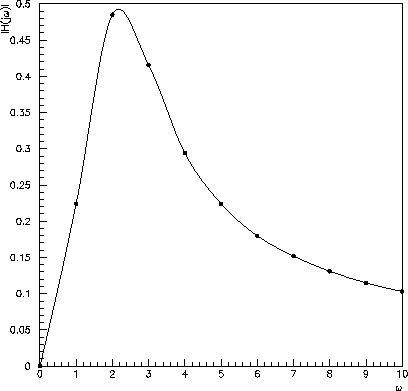
Figure 3.6: The transfer function from the table above.
- If
, what is the approximate value of
at its highest point?
If
then
at
is
. Therefore